pagerank 算法实现

一个好的搜索引擎是现如今面向互联网编程的重要工具。而pagerank是曾经谷歌用来确定搜索引擎网页排名的算法，算法足够简洁且实用，且采用集群进行分布式计算而不是小型机的方法，给当时的网页排名带来了革命性突破。如果你实在看不懂理论部分如何处理的，就想当初的我一样。建议好好看一下代码，一目了然。

算法思想

这个算法十分简单，核心思想是『用投票的方法来确定哪个网页的质量好』，可以画几张图就描述清楚。

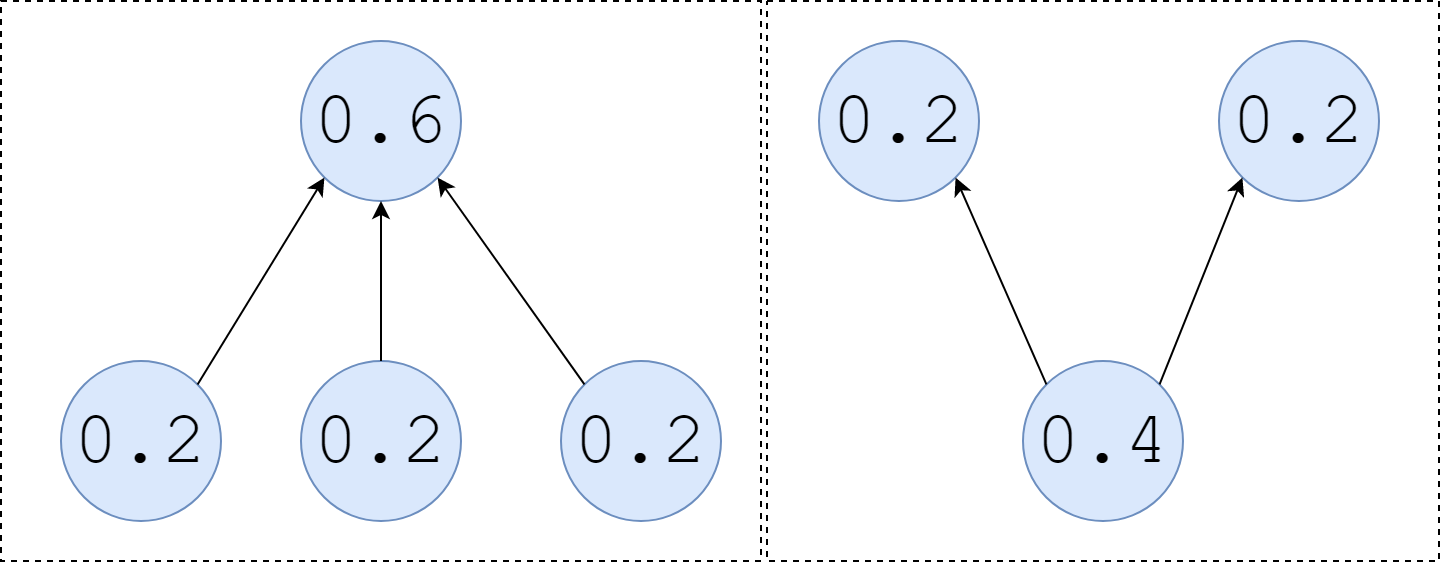
• 如上图所示，当三个评分为0.2的网页指向一个网页时，那个网页的评分就是0.6；
• 当一个0.4评分的网页指向两个网页时，那两个网页平分分数，都是0.2。

算法将整个互联网，看做一张有向图，网页是图上的点，链接是图上的有向边。每个网页都有一个分数，称作 PageRank，可以把它当做是一种「投票权」，将每一个链接作为一次「投票」，每个网页的 PageRank 等于所有指向该网页的网页的 PageRank 的求和。如果一个网页被指向的次数很多，且分数很大，那么就认为这个网页是被投票选出来的高质量网页；反之是广告等流氓网页。

环形处理

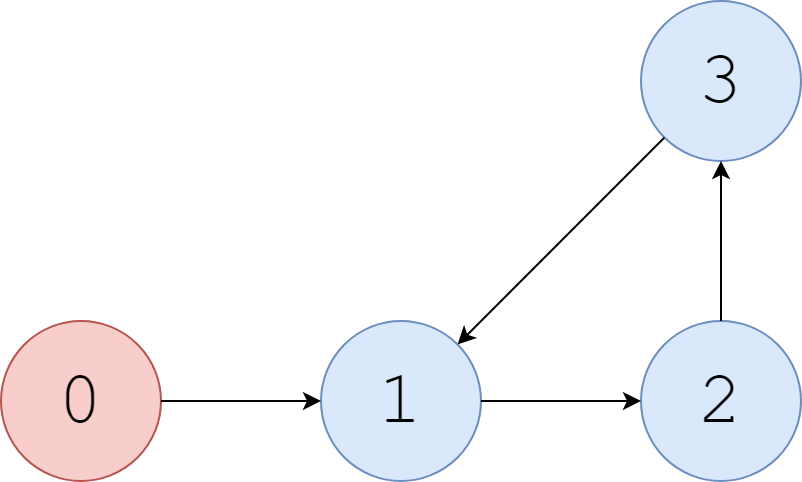
如果是这样的网页，1号网页指向2号网页，2号网页指向3号网页，3号网页又指回1号网页。这个环路会一直循环，分数会持续叠加。这样的结果肯定不正确。为了处理环路，论文中指出：当用户在浏览网页时，有$\alpha$的概率沿着链接去访问下一个网页；$1-\alpha$的概率直接关闭网页去看其他网页。那么问题就迎刃而解了，设置随机数，来确定沿着链接访问网页还是访问其他的网页。处理环路的代码如下：

import numpy as np


class pagerank(object):
    def __init__(self, alpha=0.15, num=1000):
        self.__alpha = alpha
        self.__num = num

    def run(self):
        # 邻接矩阵
        adj = np.array(([0, 1, 0, 0], [0, 0, 1, 0], 
                        [0, 0, 0, 1], [0, 1, 0, 0]))
        cnt = [0 for i in range(4)]
        # 最开始访问的页面
        page = np.random.randint(0, 4, 1)
        for i in range(self.__num):
            tmp = np.random.random()
            # 页面内选择
            if tmp > self.__alpha:
                page = np.where(adj[page] == 1)[0][0]
                cnt[page] += 1
            # 随机游走
            if tmp <= self.__alpha:
                page = int(np.random.randint(0, 4, 1))
                cnt[page] += 1

        return cnt


alpha, num = 0.15, 1000
page_num = pagerank(num=num, alpha=alpha)
cnt = page_num.run()

# 百分比表示某个时间点查看某个页面的概率
page_pro = [str(i / num * 100) + '%' for i in cnt]
print(page_pro)

而最后用百分比来表示某个页面在某一个时间段内被查看的概率，就可以按照概率的大小来确定网页排名了。结果大概是：

0: 0.04
1: 0.33
2: 0.32
3: 0.3

一般化

Step1：假设得到$N$个网页，所有的网站的初始排名是$B_0=(\frac{1}{N},\frac{1}{N},…,\frac{1}{N})^T$。

Step2：矩阵$A$是网页之间的链接数目，得到这个矩阵并不难，只要有个爬虫机器人就好了。

Step3: 更新网页排名分数：$B_{i+1}=\alpha A B_i + (1−\alpha)B_0$ 。公式第一项为其他页面沿着链接访问该页面的分数，第二项为直接跳转到该页面的分数。

Step4：迭代计算直至$|B_{i+1}−B_i|<\epsilon$，或者制定迭代轮数，可以得到最终结果。（选排名前几的就可以了）

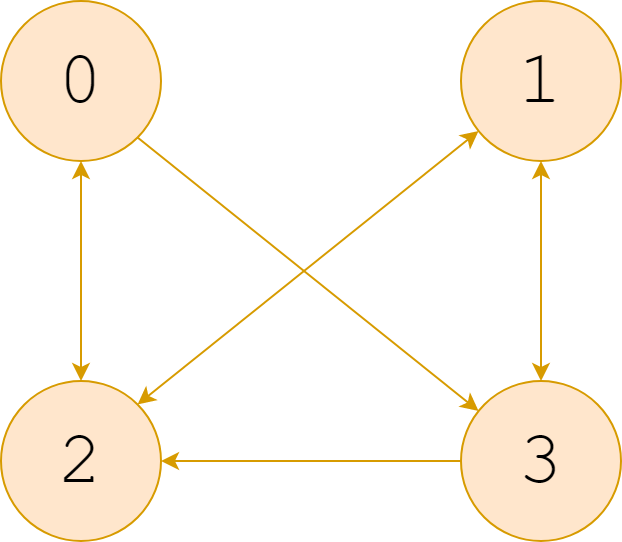
对于上图，一个完整的 pagerank 算法代码如下所示：

import numpy as np


class pagerank(object):
    def __init__(self, adj, alpha=0.15, num=1000):
        self.__adj = adj
        self.__alpha = alpha
        self.__num = num
        self.__page_num = self.__adj.shape[0]

    def run(self):
        # 均匀设置分数
        score = [1 / self.__page_num for i in range(self.__page_num)]

        # 看看有哪些页面指向自己
        point_to_self = [
            list(np.where(self.__adj[:, i] == 1)[0])
            for i in range(self.__page_num)
        ]

        # 如果四个页面，3号页面指向1号页面和2号页面，那么转移到任何一个页面的概率要平分
        point_to_other = [
            s / np.where(self.__adj[i, :] == 1)[0].size
            for i, s in enumerate(score)
        ]

        # 均匀跳转概率
        jump_pro = 1 / self.__page_num

        # 网页访问 num 次，计算每个页面的概率
        for num in range(self.__num):
            for i in range(self.__page_num):
                s = sum(point_to_other[j] for j in point_to_self[i])
                # 其它页面指向自己，加上跳转概率，就是自己被访问的概率
                score[i] = s * (1 - self.__alpha) + self.__alpha * jump_pro
            # 访问一次后，指向其它页面的概率更新，也就是再次均匀划分
            point_to_other = [
                s / np.where(self.__adj[i, :] == 1)[0].size
                for i, s in enumerate(score)
            ]
        return score


if __name__ == "__main__":

    # 邻接矩阵
    adj = np.array([[0, 0, 1, 1], [0, 0, 1, 1], [1, 1, 0, 0], [0, 1, 1, 0]])
    assert adj.shape[0] == adj.shape[1]
    alpha = 0.15
    num = 1000

    p = pagerank(adj, alpha=alpha, num=num)
    score = p.run()

    page_pro = [str(round(i * 100, 2)) + '%' for i in score]
    print(page_pro)

完整代码

• 数据集（把数据集直接复制粘贴保存为link.data）
• 数据集说明：https://amslaurea.unibo.it/10469/1/Temporal_PageRank.pdf
• 代码链接：https://github.com/yuanjie-ai/Spark-learn/blob/main/pagerank-demo/main.py

我做出来的结果是下面这样的，和网上公布的大多结果保持一致。

# 节点数量
vertex number is : 183811
# 边的数量
edge number is : 641727
# 迭代 100 轮执行时间
33.12673735618591
# 排名前几的结果
WT21-B37-76 0.0014513384131756468
WT21-B37-75 0.0008265334385338406
WT25-B39-116 0.0007959759004498566
WT23-B21-53 0.000743342282644727
WT24-B40-171 0.0006743921148099952
WT23-B39-340 0.000671900553656238
WT23-B37-134 0.0006528246305109245
WT08-B18-400 0.000619414607912892
WT13-B06-284 0.0006092497992106295
WT24-B26-46 0.0005877279600700914
WT13-B06-273 0.0005658734074429803
WT01-B18-225 0.0005354041130099478
WT04-B27-720 0.0005072144885359412
WT23-B19-156 0.0004843699050803331

参考

https://liam.page/2017/04/04/Python-100-lines-of-PageRank/